07 - Weighting Euclidean Distance
In 06 - Matching in Euclidean Distance, we saw how you can match multiple numeric variables by Euclidean distance. However, you might still want to match some of those variables more closely than others. We can do this with weights.
Setup
Load Packages
library(tidyverse)
library(LexOPS) # package with functions for item-wise matchingImport the Data
stim_pool <- read_csv("stim_pool.csv")Matching in Euclidean Distance
Step 1: Find Matches
As in 06 - Matching in Euclidean Distance, we’ll match face width, face length, and task response time in Euclidean space. However, we decide that we want to weight these controls differentially, because some are more important to match than others. Specifically, we decide that:
- Face width is the most important variable to match
- Face length is kind of important to match
- Task response time is useful to match, but least important
We can pass weights, reflecting the relative importance of the controls, to control_for_euc(). These weights should be a vector of numbers in the same order as the variables given as controls. Importantly, it’s the relative sizes of the weights that matters - they will be automatically scaled by LexOPS so we don’t have to change our overall tolerance (-0.5:0.5).
stim <- stim_pool %>%
set_options(id_col = "stim_id") %>%
# create the three levels of age
split_by(age, 1:28 ~ 35:45 ~ 50:100) %>%
# control for all variables
control_for_euc(c(face_width, face_length, task_rt), -0.5:0.5, weights = c(10, 5, 2)) %>%
control_for(gender) %>%
generate(n=100, seed=42, match_null="inclusive")## Generated 5/100 (5%). 9 total iterations, 0.56 success rate.
Generated 10/100 (10%). 16 total iterations, 0.62 success rate.
Generated 15/100 (15%). 23 total iterations, 0.65 success rate.
Generated 20/100 (20%). 33 total iterations, 0.61 success rate.
Generated 25/100 (25%). 44 total iterations, 0.57 success rate.
Generated 30/100 (30%). 52 total iterations, 0.58 success rate.
Generated 35/100 (35%). 64 total iterations, 0.55 success rate.
Generated 40/100 (40%). 75 total iterations, 0.53 success rate.
Generated 45/100 (45%). 83 total iterations, 0.54 success rate.
Generated 50/100 (50%). 93 total iterations, 0.54 success rate.
Generated 55/100 (55%). 104 total iterations, 0.53 success rate.
Generated 60/100 (60%). 114 total iterations, 0.53 success rate.
Generated 65/100 (65%). 128 total iterations, 0.51 success rate.
Generated 70/100 (70%). 138 total iterations, 0.51 success rate.
Generated 75/100 (75%). 150 total iterations, 0.50 success rate.
Generated 80/100 (80%). 162 total iterations, 0.49 success rate.
Generated 85/100 (85%). 174 total iterations, 0.49 success rate.
Generated 90/100 (90%). 185 total iterations, 0.49 success rate.
Generated 95/100 (95%). 194 total iterations, 0.49 success rate.
Generated 100/100 (100%). 205 total iterations, 0.49 success rate.As before, this gives us a list of matched triplets of young, middle-aged, and old faces. Each row has a young face A1, a middle-aged face A2, and an old face A3.
stim## # A tibble: 100 x 5
## item_nr A1 A2 A3 match_null
## <int> <chr> <chr> <chr> <chr>
## 1 1 face_1974 face_1323 face_3571 <NA>
## 2 2 face_4690 face_1465 face_163 <NA>
## 3 3 face_4758 face_4083 face_4762 <NA>
## 4 4 face_2965 face_2527 face_4021 <NA>
## 5 5 face_4439 face_345 face_3077 <NA>
## 6 6 face_1207 face_3714 face_2455 <NA>
## 7 7 face_1700 face_493 face_1198 <NA>
## 8 8 face_3803 face_1182 face_1709 <NA>
## 9 9 face_3464 face_537 face_4372 <NA>
## 10 10 face_2064 face_4458 face_1381 <NA>
## # ... with 90 more rowsStep 2: Check Stimuli
We can check the values for each item with long_format():
long_format(stim)## # A tibble: 307 x 7
## item_nr condition match_null stim_id gender age control_map_1
## <int> <chr> <chr> <chr> <chr> <dbl> <chr>
## 1 1 A1 <NA> face_1974 m 24 0
## 2 1 A2 <NA> face_1323 m 43 0.273218812990132
## 3 1 A3 <NA> face_3571 m 57 0.490728856072509
## 4 2 A1 <NA> face_4690 m 18 0.196491173340288
## 5 2 A2 <NA> face_1465 m 40 0.378832631634821
## 6 2 A3 <NA> face_163 m 50 0
## 7 3 A1 <NA> face_4758 m 20 0.396889229473117
## 8 3 A2 <NA> face_4083 m 40 0
## 9 3 A3 <NA> face_4762 m 60 0.479637465327233
## 10 4 A1 <NA> face_2965 f 24 0
## # ... with 297 more rowsTo check the matching of the variables that the Euclidean distance is calculated from, we can pass the variables to plot_design():
plot_design(stim, c("face_width", "face_length", "task_rt"))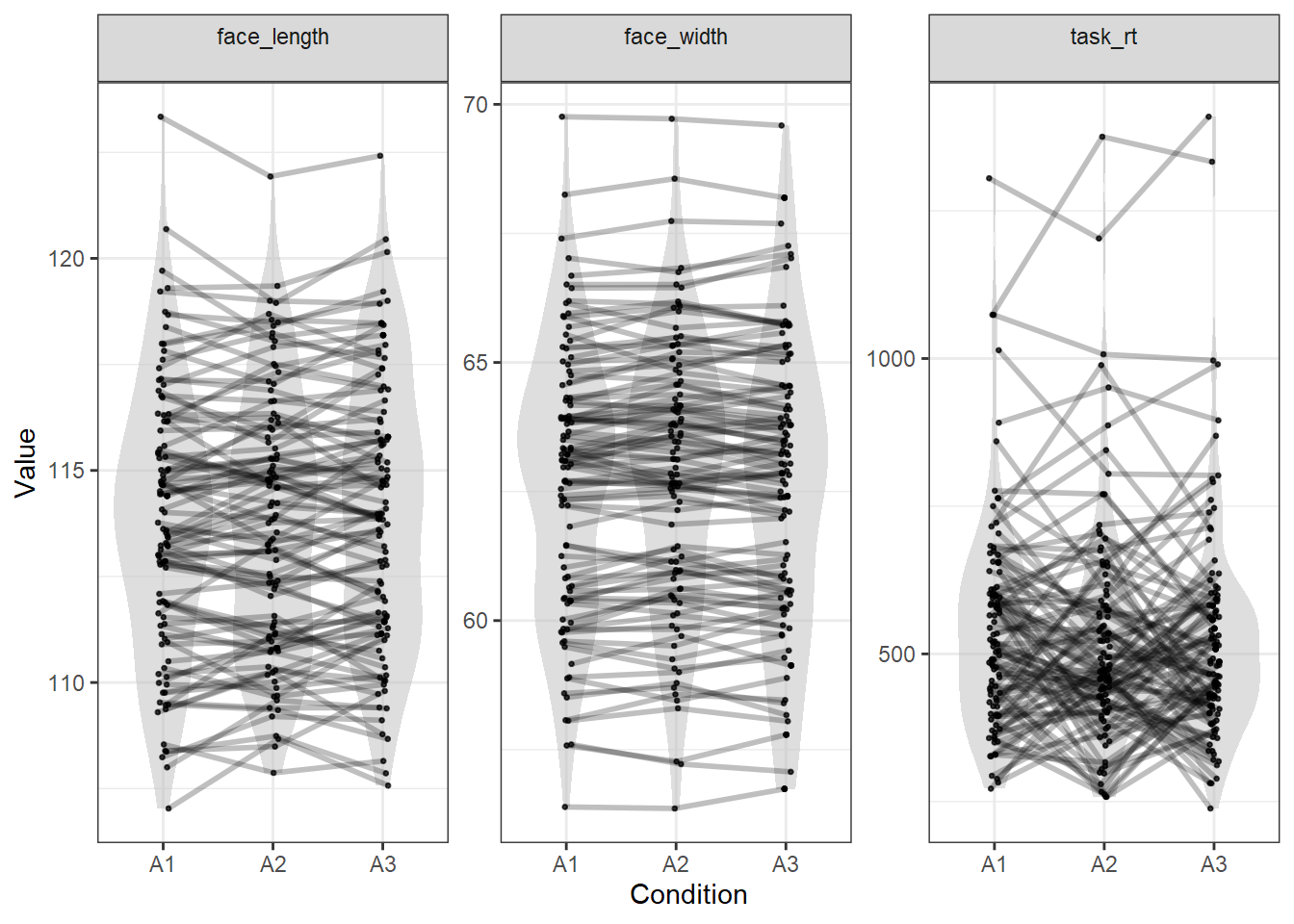
As you can see, this time the precision with which the three variables are matched reflects the relative sizes of the weights we gave, where face width is matched very closely, face length is matched quite closely, and task response time is matched very loosely.