02 - Minimising the Kolmogrov-Smirnov Statistic
In this example, I show how you can match two conditions on the distribution of one confounding variable using the Kolmogrov-Smirnov (K-S) statistic. This statistic is equal to the maximum difference in the cumulative probability of two distributions. It’s frequently used to check distributional assumptions - for example, the K-S test is often used to check normality by comparing the cumulative probability of a sample’s distribution to that expected with a normal distribution (i.e., pnorm()). Conveniently for us, however, it can also be used to compare to separate empirical samples, to measure how different the distributions are in an assumption-free manner.
For comparison, the code here is very similar to that in 01_max_distributional_overlap.Rmd.
Setup
Load Packages
library(tidyverse)Import the Data
stim_pool <- read_csv("stim_pool.csv")Matching Using K-S Statistic
Let’s create a list of 100 young and 100 old faces, matched on face width. To match the conditions, we’ll minimise the Kolmogrov-Smirnov statistic between the face_width distributions in each condition.
Step 1: Identify conditions
First, we define our conditions. Let’s say young faces are <28 years old, and old faces are >50 years old. We can use dplyr’s mutate() and case_when() to create our conditions.
stim_pool <- mutate(stim_pool, cond = case_when(age<28 ~ "young", age>50 ~ "old"))This gives us >1000 candidate items for each of our conditions.
count(stim_pool, cond)## # A tibble: 3 x 2
## cond n
## <chr> <int>
## 1 old 1116
## 2 young 1202
## 3 <NA> 2682Step 2: Create a vector of seeds
Before we can start with the simulations, we need to make sure our datasets will be reproducible. We can do this by creating a vector of seeds which will be used to select our stimuli. Random seeds make the random number generator give reproducible results. If we want to run 1000 simulations, this code will create a vector of 1000 random seeds for us. Random seed values can be any integer (whole number) we can represent in R. The smallest possible seed is 1, and we can use .Machine$integer.max to get the maximum possible seed number R will let us represent.
I also set the seed first so the result are reproducible, but feel free to comment that out if you would like to get a different result to mine.
set.seed(43) # comment this line out (put # at the start of the line) to get a different result to mine
n_iter <- 1000
seeds <- sample(1:.Machine$integer.max, n_iter)Step 3: Simulate a large number of samples
We want to simulate a large number of random samples. On each iteration, we can record the Kolmogrov-Smirnov statistic for the two conditions’ distributions of face width. The ks.test() function is part of the stats package, which is included with the standard installation of R. This function gives us an annoying warning about the p-value. Since we’re not using the p-value at all, we can suppress this warning to avoid spamming our consoles with 1000 identical warnings. We can use map_df() to loop over our seeds and record the K-S values from each iteration in a large dataframe.
For speed, I’m only running 1000 iterations in this example, but I recommend running much larger numbers of iterations to improve the quality of the match.
Depending on how many iterations we run, this could take a long time.
res <- map_df(seeds, function(seed_i) {
# set the seed, so we can recreate any sample later
set.seed(seed_i)
sample <- stim_pool %>%
# only keep observations from conditions we are interested in (remove faces from ages 29 to 49)
filter(cond %in% c("young", "old")) %>%
# for each condition, randomly select 100 items
group_by(cond) %>%
slice_sample(n = 100)
# get the face_width values for the young condition in this sample
face_width_young <- sample %>%
filter(cond == "young") %>%
pull(face_width)
# get the face_width values for the young condition in this sample
face_width_old <- sample %>%
filter(cond == "old") %>%
pull(face_width)
# get the Kolmogrov-Smirnov statistic for the two conditions' distributions in the control variable
# use suppressWarnings() to silence the annoying warning about p-values
ks_results <- suppressWarnings( ks.test(face_width_young, face_width_old) )
# extract the actual value for the K-S statistic
ks_value <- ks_results$statistic
# return a row of the dataframe with the seed and K-S value
tibble(seed = seed_i, ks = ks_value)
})Step 4: Check the results
We can now look at the distribution of K-S values from all the random samples. The closer to 0, the more similar the two conditions’ distributions are in cumulative probability. I’ve added the points below the distribution to show the results from each individual sample.
ggplot(res, aes(ks)) +
geom_density() +
geom_point(aes(y = -1), position = position_jitter(height=1)) +
xlab("Kolmogrov-Smirnov Statistic")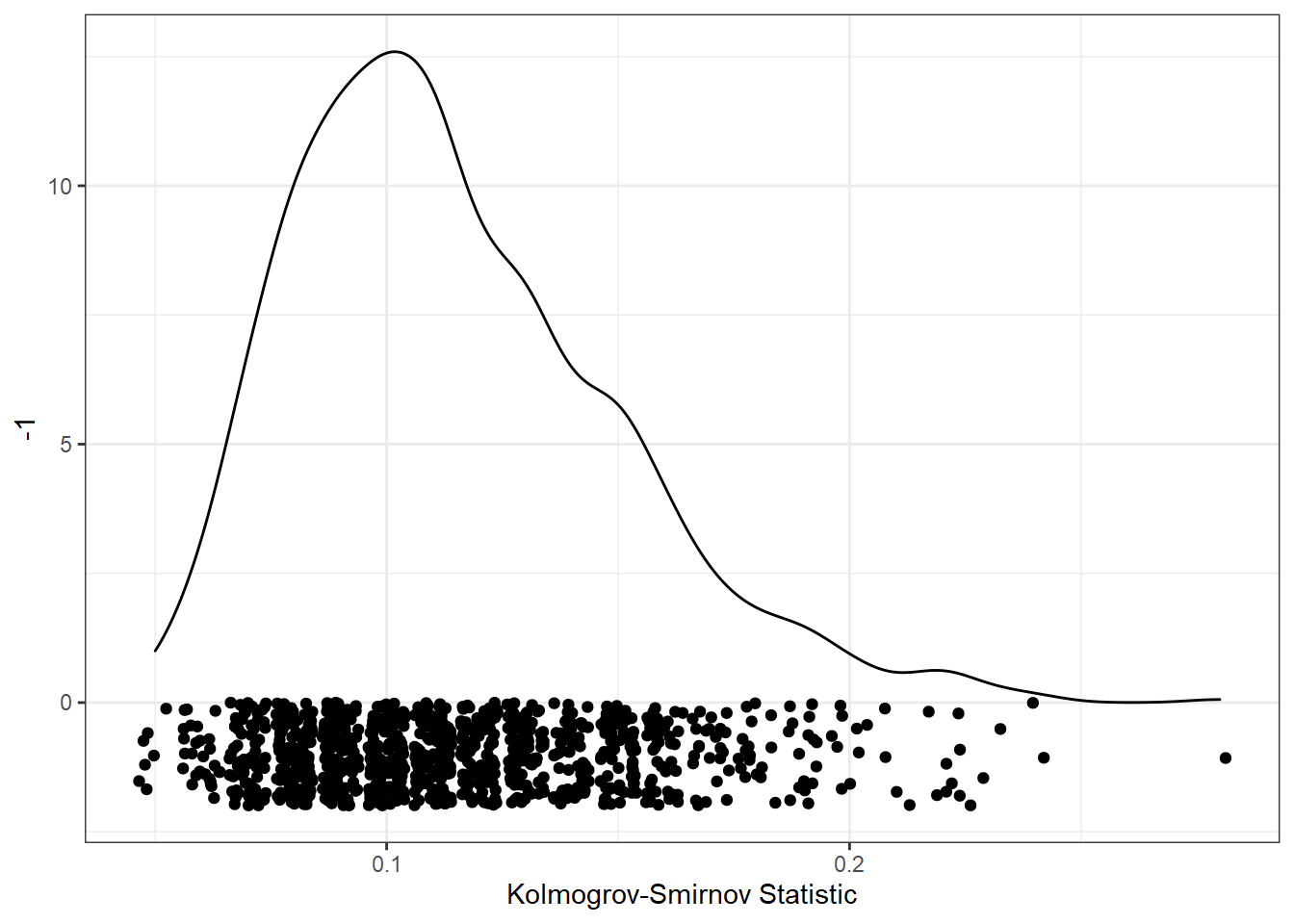
Step 5: Find the best stimulus set
We can now sort the results by the K-S statistic (ascendingly) to order them by how well-matched the conditions are in each candidate stimulus set.
res_sorted <- arrange(res, ks)
res_sorted## # A tibble: 1,000 x 2
## seed ks
## <int> <dbl>
## 1 449694146 0.05
## 2 2128417332 0.05
## 3 1225755600 0.05
## 4 88982956 0.05
## 5 748533543 0.05
## 6 552760850 0.05
## 7 1662335796 0.05
## 8 1346472709 0.06
## 9 2130184978 0.06
## 10 1867190100 0.06
## # ... with 990 more rowsNow we can just extract the best seed as that which has the lowest K-S statistic.
# sort by distance ascendingly, so the best seed is at the top, and extract it
best_seed <- res_sorted %>%
pull(seed) %>%
first()
best_seed## [1] 449694146Step 6: Recreate the best stimulus set
Now we know that 449694146 is the best seed, we can use that seed to recreate the stimulus set. This code needs to be identical to our simulation code to ensure we recreate the exact same stimulus set.
set.seed(best_seed)
best_stim <- stim_pool %>%
filter(cond %in% c("young", "old")) %>%
group_by(cond) %>%
slice_sample(n = 100)To prove that the stimuli are well-matched on face width, here is what the distribution of face_width looks like for each condition:
ggplot(best_stim, aes(face_width, colour=cond, fill=cond)) +
geom_density(alpha=0.4)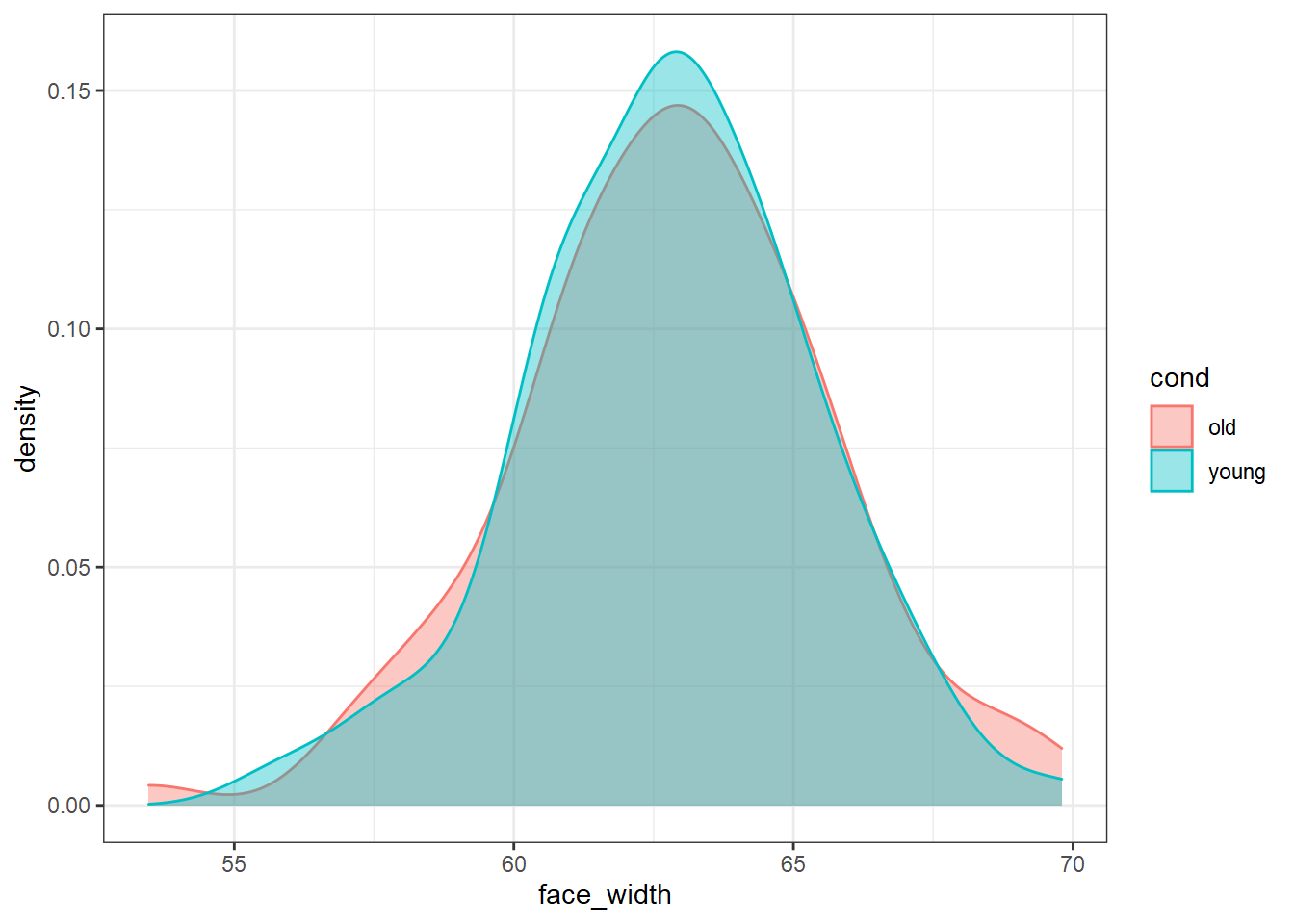
We could use the faces in best_stim for our experiment, and be fairly sure that we’ve controlled for face width.
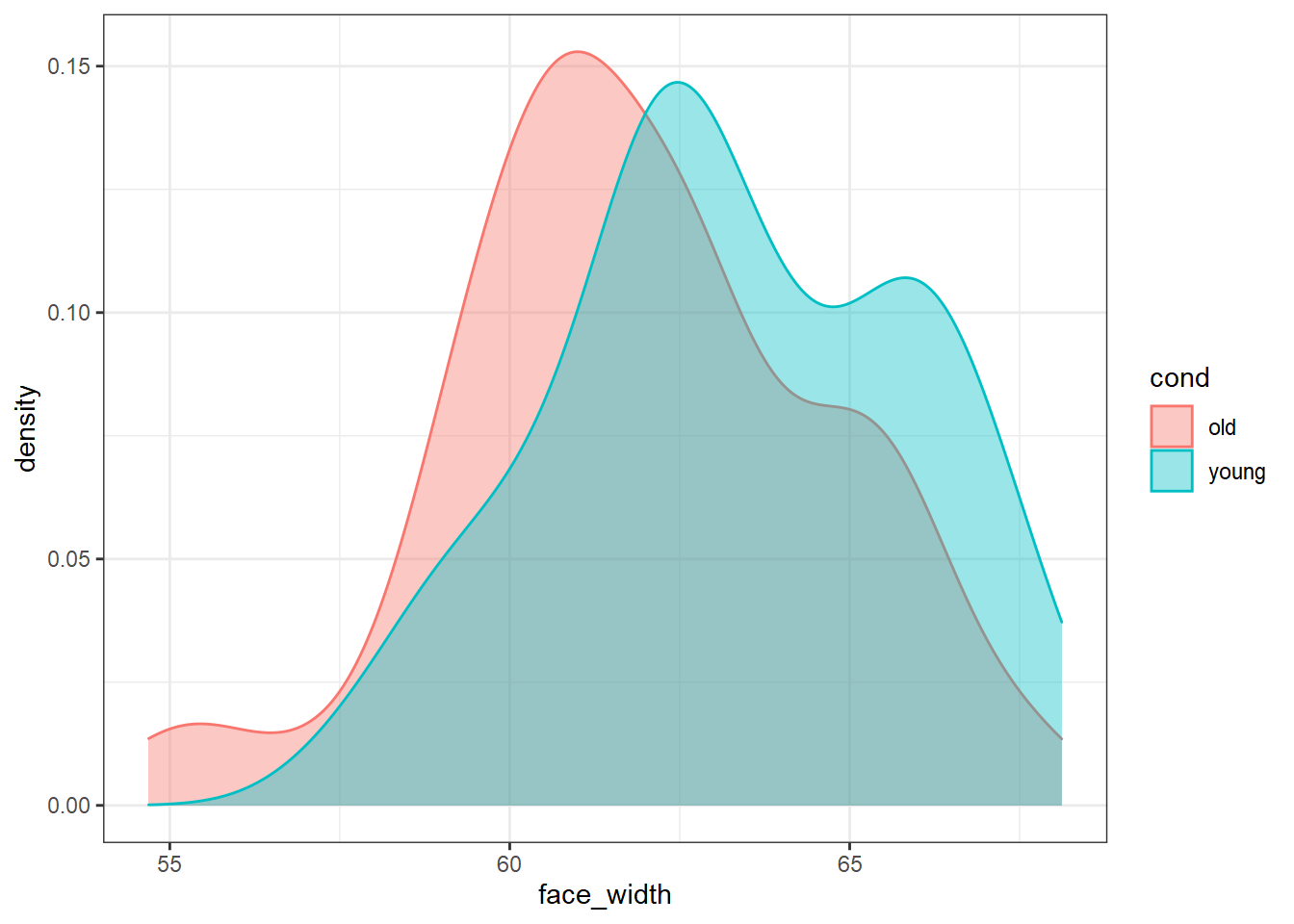
For comparison, here is what the worst stimulus set looks like:
# sort descedningly (smallest K-S statistic first), and extract the top seed
worst_seed <- res_sorted %>%
arrange(desc(ks)) %>%
pull(seed) %>%
first()
set.seed(worst_seed)
# recreate the worst stimulus set
worst_stim <- stim_pool %>%
filter(cond %in% c("young", "old")) %>%
group_by(cond) %>%
slice_sample(n = 100)
ggplot(worst_stim, aes(face_width, colour=cond, fill=cond)) +
geom_density(alpha=0.4)